Posted on

Why Our Computer Software Helps Kids Improve Their Math Understanding

And why most “educational” software doesn’t…

The trouble with most so-called “educational software” for teaching math is that is was designed by a programmer or a business owner, not an educator. As a result, it was designed to connect questions with answers really fast, in the mistaken belief that if you could just automate the testing of students on matching question and answer, they would learn faster and better.

Yeah, so what?

Trouble is, most of the math adults use in real problem solving involves figuring out what math is needed, finding the best tools to use, then applying them and evaluating the result. If the chosen tools do not produce a solution, then alternative pathways are tried, until the solution is reached.

Very little actual use of mathematics involves memorizing and single fact in response to a simple question, which is exactly what is targeted by most math software.

A New Pedagogy: Provide Tools to Support Thinking

Let me introduce a new set of interactive, cross-platform teaching and learning tools, which we call Professor Pete’s Gadgets.

Professor Pete’s Gadgets are designed to interactively support students’ development of mathematical thinking, by presenting them with symbols, pictures and words which they can manipulate to understand how they relate to each other. It is a fantastic teaching tool that, combined with well sequenced lessons and worksheets, allow students to understand the math concept.

For example, they can see how common fractions, percentages, decimal fractions and ratios relate to each other, what they look like in a pictorial form and where they sit on a number line between 0 and 1:

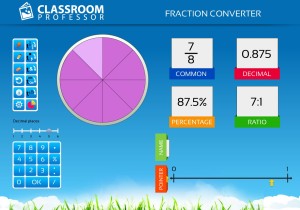
Professor Pete’s Gadgets: Fraction Converter

Posted on

Khan Academy: “Teacher-Proof” Curriculum?

I follow Dan Meyer’s blog quite closely, and find the discussions over there really stretch my thinking sometimes about how we teach math, and the best ways to engage students in thinking.

Dan Meyer on the Khan Academy

I first encountered Salman Khan on his TED video, perhaps like lot of others. (Incidentally, that’s also how I first heard of Dan Meyer, watching his TED talk.) I found Sal Khan’s methods surprising and challenging, and incidentally, his business practices pretty remarkable also. If you look at his site, it’s hard not to be impressed by the sheer volume of material he has there, with a huge list of videos, all free for watching.

Recently Dan has posted a couple of articles about the Khan Academy:

Dan points out several really important points about the Khan academy’s approach, including an apparent shift in emphasis from supporting the work of teachers via flipped lessons to supplying an entire curriculum for students. Crucially, Dan comments that students actually find watching the Khan videos quite boring, which surely is a critical flaw in the program.

“Flipped Classes” – a Solution to Bad Teaching?

To summarise, in case you haven’t been keeping up with this debate, the idea put forward by Khan at the TED conference which has captured the attention of many educators, is “flipped classes”. In this model, instead of the teacher teaching in class and then assigning practice work for homework, students watch the teaching at home via Khan’s videos online, then in class the teacher gets to follow up the video presentation, offer one-on-one tutoring help, and generally support and troubleshoot students’ learning, freed from having to spend hours planning and teaching didactic lessons.

What’s the philosophical idea behind Khan’s approach? Note the low-tech quality of the videos: it can’t be able visual engagement, hooking students with exciting music, animations or the like. No, what Khan is attempting, without really admitting it, is to produce a set of perfect teaching videos. If you like (and I doubt you do), a teacher-proof syllabus. How does that strike you? I find it insulting: why does Mr Khan feel that a disembodied voice track and a screen showing the teacher’s written notes for a math process is better than what real teachers do in a real, physical classroom, with students who are present in the same space?

The only way to accept KA as a replacement for what teachers in general do in classrooms is if you subscribe to the idea that most teachers suck at teaching math. If that premise is accepted, then the idea that a single source of “expert instruction”, delivered uniformly to all students, could supply all the teaching might look pretty attractive.

However, critics point out, often with some heat and passion, that there are several problems with this scenario:

  • lecturing to students is not the best pedagogical approach to teaching
  • video recordings lock every student into a single lesson for each topic
  • there is no opportunity for students to ask questions of the video teacher, to have something explained again, other than replaying that part of the video

What do you think?