I recently posted the following graphic on my Facebook page:
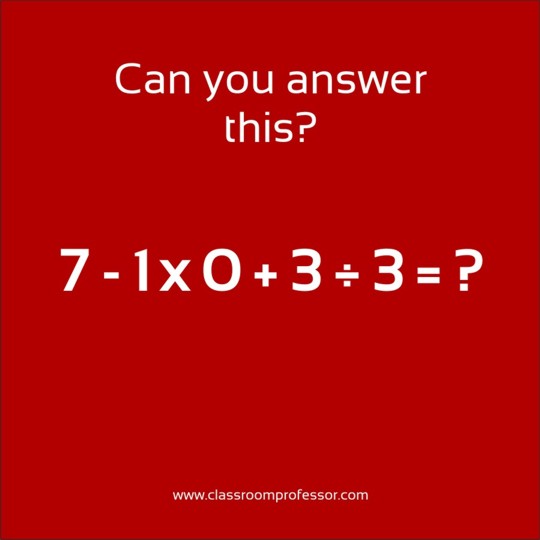
Having taught many classes of primary/elementary students, I have taught my fair share of lessons on the Order of Operations. To me, the rules for applying operations in the correct order are not that difficult:
- Process whatever is in brackets first (applying later rules if necessary)
- Apply “other” operations such as indices/powers or square roots.
- Apply multiplication and division, in order as they appear from left to right.
- Apply addition and subtraction, in order as they appear from left to right.
The reason for having these rules, of course, is so that we can all agree on the value equal to an expression with multiple operations. Otherwise, we would have ambiguous situations, which would be highly inconvenient, to say the least. For example, how should we evaluate the following:
2 + 5 x 7 = ___
- If we work in order from left to right, we get 49: 2 + 5 = 7; 7 x 7 = 49
- If we apply multiplication first, then addition, we get 37: 5 x7 = 35; 2 + 35 = 37. This is the correct answer, but only because we collectively agree that we should carry out multiplication before addition.
My intention with the Facebook post was to generate interest, attract people to “Like” the page, start conversations, and so on. My Facebook page at that time had around 150 people who had “liked” it, and I was used to seeing around 100 interactions a day on the page. I was unprepared for what happened in the following 2 weeks:
- over 70,000 people in all saw the post
- over 6000 people left comments
- more than 140 shared it with their followers on Facebook
- over 400 liked the post
- more than 15,000 interacted with the post
Apparently, this question caught the interest of a lot of people on Facebook, and many felt the need to respond (which was the whole idea, of course). I guess almost all adults learned to answer questions like this at school, and over 6000 who saw it were confident enough in their abilities to answer it in public. I presume they believed they were correct with their answer, and in fact several backed up their numerical response with comments emphasizing that they believed with great confidence that they were correct:
- “8 use BODMAS”
- “… and in arithmetic you apply the multipliers and dividers first, then the additions/subtractions afterwards, so the answer is 8”
- “7-(1×0) + (3/3) = 7-0+1 = 8”
- “YOU GUYS ARE SO DUMB YOU HAVE TO USE FREAKIN ORDER OF OPERATIONS SO ITS 8, im seventh grader and i got that right and adults cant WOW”
Most amusingly (or worryingly), even those who were incorrect often tried to justify their responses:
- “it’s 4 you idiots”
- “It is 6 if you apply principle of BoDMAS”
- “6 do the BODMAS rule! Brackets first then in order, pOwers, Division, Multiplication, Addition, Subtraction!”
- “1 because 7-1=6×0=0+3=3/3=1 SIMPLES”
- “PEMDAS 1*0= 0 / 3=0 +3=3-7= -4”
- “Think you all need to go back to school. Anything X 0 is 0…!!!!!!!”
Seeing the huge number of responses I thought it would be interesting to analyze them to see just how good today’s Facebook users are at primary / elementary level arithmetic. The results were, to say the least, disappointing:
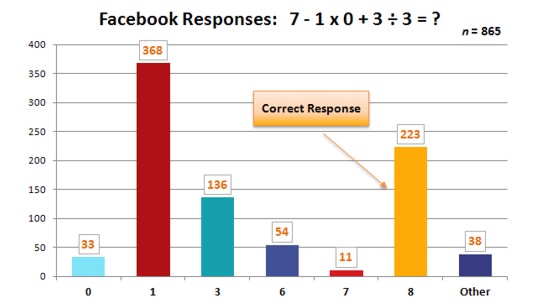
All up, out of the sample of 865 responses which were analyzed, just 25.8% of responses were correct. Of the three-quarters of incorrect responses:
- 43% of respondents apparently applied the operations strictly in order from left to right: 7 – 1 = 6; 6 x 0 = 0; 0 + 3 = 3; 3 ÷ 3 = 1
- 16% of responses were 3. This may have been the result of ignoring the “multiplying by 0”, getting (6 + 3) ÷ 3 = 3
- 6% of answers were 6, perhaps because the respondent made a mistake in calculating 3 ÷ 3
- 4% of respondents gave the answer 0. A number of people explained that “anything multiplied by zero equals zero”, evidently applying that to the entire expression
I have some ideas about why this little experiment found just 26% of Facebook users who saw and responded to the question could answer it correctly. What do you think? Are we teaching the order of operations badly? Should we even bother to teach it, since it seems not to be successful?
Leave a comment below to say what you think:
