I recently posted the following graphic on my Facebook page:
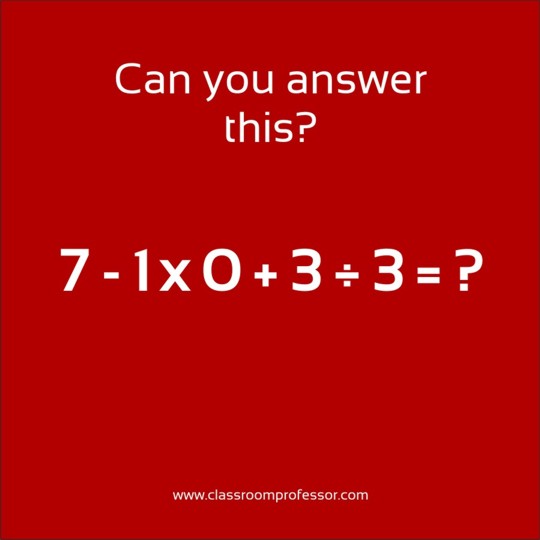
Having taught many classes of primary/elementary students, I have taught my fair share of lessons on the Order of Operations. To me, the rules for applying operations in the correct order are not that difficult:
- Process whatever is in brackets first (applying later rules if necessary)
- Apply “other” operations such as indices/powers or square roots.
- Apply multiplication and division, in order as they appear from left to right.
- Apply addition and subtraction, in order as they appear from left to right.
The reason for having these rules, of course, is so that we can all agree on the value equal to an expression with multiple operations. Otherwise, we would have ambiguous situations, which would be highly inconvenient, to say the least. For example, how should we evaluate the following:
2 + 5 x 7 = ___
- If we work in order from left to right, we get 49: 2 + 5 = 7; 7 x 7 = 49
- If we apply multiplication first, then addition, we get 37: 5 x7 = 35; 2 + 35 = 37. This is the correct answer, but only because we collectively agree that we should carry out multiplication before addition.
My intention with the Facebook post was to generate interest, attract people to “Like” the page, start conversations, and so on. My Facebook page at that time had around 150 people who had “liked” it, and I was used to seeing around 100 interactions a day on the page. I was unprepared for what happened in the following 2 weeks:
- over 70,000 people in all saw the post
- over 6000 people left comments
- more than 140 shared it with their followers on Facebook
- over 400 liked the post
- more than 15,000 interacted with the post
Apparently, this question caught the interest of a lot of people on Facebook, and many felt the need to respond (which was the whole idea, of course). I guess almost all adults learned to answer questions like this at school, and over 6000 who saw it were confident enough in their abilities to answer it in public. I presume they believed they were correct with their answer, and in fact several backed up their numerical response with comments emphasizing that they believed with great confidence that they were correct:
- “8 use BODMAS”
- “… and in arithmetic you apply the multipliers and dividers first, then the additions/subtractions afterwards, so the answer is 8”
- “7-(1×0) + (3/3) = 7-0+1 = 8”
- “YOU GUYS ARE SO DUMB YOU HAVE TO USE FREAKIN ORDER OF OPERATIONS SO ITS 8, im seventh grader and i got that right and adults cant WOW”
Most amusingly (or worryingly), even those who were incorrect often tried to justify their responses:
- “it’s 4 you idiots”
- “It is 6 if you apply principle of BoDMAS”
- “6 do the BODMAS rule! Brackets first then in order, pOwers, Division, Multiplication, Addition, Subtraction!”
- “1 because 7-1=6×0=0+3=3/3=1 SIMPLES”
- “PEMDAS 1*0= 0 / 3=0 +3=3-7= -4”
- “Think you all need to go back to school. Anything X 0 is 0…!!!!!!!”
Seeing the huge number of responses I thought it would be interesting to analyze them to see just how good today’s Facebook users are at primary / elementary level arithmetic. The results were, to say the least, disappointing:
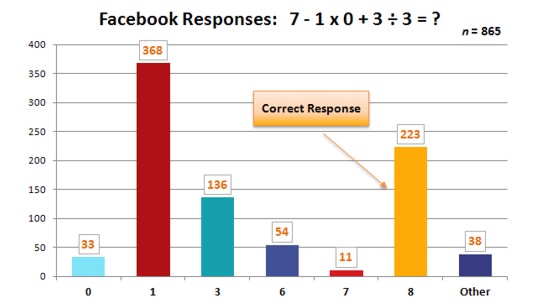
All up, out of the sample of 865 responses which were analyzed, just 25.8% of responses were correct. Of the three-quarters of incorrect responses:
- 43% of respondents apparently applied the operations strictly in order from left to right: 7 – 1 = 6; 6 x 0 = 0; 0 + 3 = 3; 3 ÷ 3 = 1
- 16% of responses were 3. This may have been the result of ignoring the “multiplying by 0”, getting (6 + 3) ÷ 3 = 3
- 6% of answers were 6, perhaps because the respondent made a mistake in calculating 3 ÷ 3
- 4% of respondents gave the answer 0. A number of people explained that “anything multiplied by zero equals zero”, evidently applying that to the entire expression
I have some ideas about why this little experiment found just 26% of Facebook users who saw and responded to the question could answer it correctly. What do you think? Are we teaching the order of operations badly? Should we even bother to teach it, since it seems not to be successful?
Leave a comment below to say what you think:

Order of operations is important in some ways, but these kinds of questions strike me as really artificial. Real mathematicians would never write an expression that way. (Of course, real mathematicians don’t usually write a lot of actual numbers anyway, but it seems much easier to see the other in an expression like ‘ab – c’ than in one like ‘a x b – c’.
I was thinking the other day about the common error where my students will think sqrt(9 + x^2) = 3 + x (distributing the root over the addition). I had a student ask me why it was wrong, and I said, you know, order of operations, but if you actually take the square root FIRST, you would get 3 + x. Knowing that the addition comes first requires understanding that the square root symbol is a kind of parenthesis or bracket (as are fractions written with a horizontal bar and a bunch of other symbols used in math).
So I think it should be taught, but I also think it’s not as obvious as it seems, and if you actually want to communicate anything by ‘7 + 1 x 0 – 3 / 3’ (or whatever) instead of specifically just test order of operations, you should just go ahead and use parentheses.
Tam, thanks for your comment.
I agree with a lot of what you’ve shared here. Order of operations is far from straightforward, yet it is important if we are to agree about the meaning of arithmetical and algebraic expressions.
The thing that troubles me is all the time we spend on teaching our students, who later when asked a math question can’t accurately apply the math they’ve been taught. To me, this points to a disconnect between HOW the math is taught and what students take away in terms of knowledge, and what they can later apply when it is needed.
I was born in 1959…..I was an A+ student in math.
However today my son gives me a math puzzle to see if I can get the answer and to my surprise I wasn’t able to get it!
I remember being taught with brackets and without brackets we simply went left to right…..do not remember being taught the “order of operations”.
I’m from Ontario, Canada
Dear Anon – I concur – also an A+ math student in Manitoba who never heard of the acronym BEDMAS or BODMAS or PEDMAS until I looked at these Facebook math questions. I believe we were taught that in the absence of brackets, work from left to right. That would explain why nearly half of the respondents answered incorrectly. I have tried to find out when the acronym was introduced as a teaching aid and Google tells me around 1912, but I know for fact I was not taught this tool.
I did A levels in 1960s and never heard of ‘order of operations’. Brackets first and then left to right. My friend studied physics at Imperial College London in early 1970s and also never heard of BODMAS. I first heard a couple of years ago from my Aussie cousin. I think it was invented in the computer age because because computer programs dont understand brackets.
Hello
No we were no taught that way either , but what l object to is the insults they dish out saying our memories have gone, we werent listening. Teachers were rubbish and theres no way l was taught that way, but we were and they cannot accept it so rude. We cannot change the past to accomodate their closed minds to another way of teaching, but accept there was another way which often they get different answers but can honestly say l never heard of it until recently on here. Why do you think they thats all of the BODMASERS wont take in and accept the truth that more people got the non BODMAS simple sum answer then them but still say we forgot. Their brains arent open to learning it actually did happen, but no we are all in denial they say, l find it very very frustrating as l cant change my answer because l was taught the easy way. We cant change the past can we lol
Hi Jean, thanks for the comment.
I, for one, do not say that you must have forgotten what you were taught. That is just a silly claim.
However, there are correct and incorrect answers in mathematics, no matter what a person learned in school. And the authority for a certain procedure comes from the field of math itself, and the experts in that field who have collectively decided what is the correct way to do math. This has nothing to do with the teaching of a particular school teacher, nor the number of commenters who believe that a certain response is correct. Thankfully, truth in mathematics is not a democracy.
Same with me . No Bodmas. School in 50s. Australia.
That is the way I was taught as well, in grade school in Kansas and California. In 5th and 6th grade in California, while most of the kids in class finished their work for the week, my teacher and I would spend the time solving math problems . He would write the problems out using the projector and I would solve them in my head usually finishing first no matter how large the equation. I do not remember being taught an order of operations before or after this time, other than do the brackets first and work from left to right.
Me too
Me too . In Australia in 1950s we were not taught pedmas.
Don’t use functional notation.
(9 + x^2)^0.5 .
Then, PEMDAS still applies, no issues.
Why it can’t be distributed has nothing to do with order of operations.
Multiplication, e.g., distributes over addition; exponentiation does not. 2 × (3 + 4) = 2×3 + 2×4, but (3 + 4) ^ 2 ≠ 3^2 + 4^2
Exponentiation *does* distribute over multiplication.
Taught BODMAS in the UK in the early 1950’s.
The issue is to ensure one method only is taught to one and all.
Folk have enough challenges with math without further unnecessary confusion.
At least two of the recent responders answered 6 and justified it like this:
1. They were smart enough to use order of operations to simplify the expression to 7 – 0 + 1.
2. One of them then mysteriously lumped the last two terms into parentheses, like this: 7 – (0 + 1). The explanation was something about “left to right,” but I don’t see how that puts parentheses into the equation. In a similar manner, the other person simply saw the minus sign following the 7 and figured that that meant that SOMETHING had to be subtracted from 7. I guess the zero didn’t qualify as that something, leaving the 1 at the end to subtract.
Very odd reasoning indeed.
Mr Toleno, thanks for the comment!
I have noticed one or two respondents attempted to use PEMDAS or BODMAS, and believed that Addition has to be done before Subtraction. When they had processed the other operations, they then had 7 – 0 + 1, which became 7 – 1 = 6.
I had encountered this with students who were still learning the rules for order of operations, but didn’t expect to see it among respondents on Facebook, who presumably have finished school for the most part.
What can we teachers do about this, do you think?
I don’t think this necessarily shows that people aren’t learning the order of operations. I know them very well, but I admit I began the equation from left to right before reminding myself.
Order of operations is important, but it isn’t something we use in everyday life, so it’s easy to forget, even if the knowledge is still there.
When I was teaching my students BODMAS on prac I used colour coded cards. Red for Brackets, Yellow for Other, Blue for Multiplication and Division, and Green for Addition and Subtraction. This puts them in a rainbow order, and also shows that Multiplication/Division and Addition/Subtraction are interchangeable. I didn’t stay long enough to see how effective this was, but I’d like to think it’s a useful technique.
Hi Sherae
Thanks for the comment. I agree that we shouldn’t read too much into this result. Order of operations are used infrequently by “regular folks” outside of math classrooms, and so it isn’t very surprising if people have forgotten how to apply the rules.
Some comments on Facebook indicated that the respondent had never heard of rules regarding the order in which to apply operations. That I find a worry, if it is true
Back in b.c. era ( before calculators), i was good at simple addition, subtraction, multiplication & division. Fifty years later i do not recall ever being taught bidmas. Granted, there could be things i can now no longer recall, but that process does not sound like one of them.
How interesting. I was looking at Yr 7 text book the other day which had order of operations in it, so I decided to see where it was in the Australian Curriculum. I checked all the levels from Yr 1 -7 and the elaborations and nowhere does it say teach “Order of Operations”. So this is left to the text book writers to infer what is meant to be taught.
My point being that many teachers are not mathematicians but will teach and do a good job of what they are told to teach. Teachers also get told that a text book is only a resource and not the curriculum. So what do teachers do – teach from a text book or interpret the curriculum as they seem fit and so maybe leave out some stuff. Point being is that the Australian Curriculum isn’t explicit enough. It is written by mathematicians for mathematicians not necessarily for the teacher who needs to know what to teach.
I fully understand the need for “order of operations” and often started teaching it just like Peter has by putting up a question and seeing the variety of answers and thereby establishing a need for an “order”. However, have I ever needed to use this information in real life – NO.
Thanks for the long, thoughtful comment, Judith!
I had to look for the topic in the Australian Curriculum, and found this under Year 6 Patterns and Algebra:
Explore the use of brackets and order of operations to write number sentences
You are quite correct, there is a tricky interplay between the curriculum and textbooks, even those that supposedly align with the curriculum. Teachers do have to know a fair bit of mathematics to expertly teach from the curriculum, and sometimes textbooks get it wrong.
As for using this in “real life”, most of us don’t need this often. But it is used in contexts such as entering formulas in a spreadsheet, for example. And I would want my students to know the basic foundations of mathematics, even if certain topics never get used explicitly by some adults in everyday life. It’s certainly a tricky question, that’s for sure.
I think the real thing to learn is that although science and math are meant to be simple and clear, they aren’t always seen that way. Being unclear for the sake of being unclear doesn’t do anything to showcase your intelligence.
http://www.thecollapsedwavefunction.com/2012/11/clarity-and-simplicity-in-science.html
Thanks for the comment, Chad, and for the link to your own article on this subject.
I’m not sure about your statement that “science and math are meant to be simple and clear”. I think for those who have developed a good level of scientific and/or mathematical reasoning (as you have), then these subjects are indeed clear.
But for a lot of folks, including many at school, this is far from the truth. Teachers, then, have a challenging job of teaching these subjects in ways that students will understand them.
Going by the results reported above, I think it’s fair to say that collectively, we math teachers haven’t done such a great job on this particular topic.
I see two major options to deal with the problem of people not learning this topic effectively at school: a) drop it from the curriculum, or b) teach it so that students understand it for themselves, and can construct an accurate, viable understanding of the topic. No doubt it’s obvious that I favour the latter option.
What I don’t agree with, however, is removing the need for rules of order of operations by always including parentheses/brackets. This will certainly make operations easier to complete, but completely neglects to teach students what to do when those grouping symbols are missing.
Thanks again for raising interesting questions!
“….but completely neglects to teach students what to do when those grouping symbols are missing.”
VERY False assumption. Who says those grouping symbols are in fact “missing”?
Maybe they were left out because they are not supposed to be there at all. Why? Because the author of the equation did not want anything prioritized.
Thats exactly my argument! You shouldn’t have to be an educated mathematician to write a simple equation. If you add brackets and priorities you are assuming what the is meant by the author of the equation. I believe that is wrong.
Oh, I don’t disagree Peter. When I say that science is simple and clear I don’t mean that you can take a superficial look at either of them and understand them completely. I even mention that it takes years of study to be proficient. What I meant was that science and math can be taught in a natural progression that is simple and easy to follow for anyone without major learning disorders.
One more correction. I’m not in favor of removing the order of operations and using a parenthesis only approach. If you’ll look in my article I actually have a footnote that says that problems like the one posed in the picture are useful when teaching the order of operations. My point was that among a general audience I’m not surprised – or necessarily alarmed – that so many would get it wrong. Should they know the order of operations? Yes. Does it mean they are mathematically illiterate? I don’t think so. It just means that we need to be more clear and efficient in the way we teach. I think you can agree with that.
Why do we have “BODMAS”?
Actually, it’s NOT because “we have to agree on something”, because we could just agree on straightforward left-to-right, avoiding the confusion of BODMAS.
We agree on the more complicated BODMAS, because it lets us write down expressions like 3X^2 + 2X – 4, without having to use a lot of brackets. Without the BODMAS convention, we would have to write the previous expression as 3 (X^2) + (2X) – 4 …
I think many students who sometimes have trouble with BODMAS, often have no trouble with expressions like 3X^2 +2X – 4, because the multiplication and exponentiation operators are left out, and this seems to “tie” the operands more closely together (although I have made the exponentiation operator explicit here since I can’t do superscripts).
If they had to evaluate expressions where the operators are explicit, they might have more trouble:
“3 x X^2 + 2 x X – 4” would probably be evaluated (given a value for X) incorrectly more frequently than the operator-implicit version. (Or maybe not: here is a research topic for someone’s Master’s thesis.)
Note also, that when you’re teaching the distributive law, you invariably hit “BODMAS confusion”. That is, when showing how multiplication/division can distribute over addition/subtraction, and how exponentiation can distribute over multiplication/division (but not addition/subtractio), you will face the following objection: “But I thought we had to do whatever is inside the brackets first!”
I haven’t found a really good — i.e. simple and obvious — way to explain this. It helps if you teach,or re-teach, distribution at the same time as you teach BODMAS, I suppose.
And you can explain that distribution is just “un-factoring”, so you can teach extracting common from all the terms of an expression, distributing them back in again, and BODMAS all at the same time.
Thanks for the comment, Douglas
I appreciate the detail you’ve added here. And it helps to know one is not alone in finding this really quite difficult to teach.
We absolutely have to agree.
We *could* agree to do it your way, which turns out to make less sense (see below). In any case, we agreed to do it this way. Centuries ago.
We could just all do it as we want to. Like, I go on red, don’t care about pedestrians in the crosswalk, etc. There’re gonna be problems.
A motive for multiplying before adding:
When you go to the store you have a list, e.g. The order of the items and quantities on the list shouldn’t affect the total # of items you buy, should it? Or, the total cost, right? If you buy 1 of something, 3 of something else, and 4 thingies:
1 x $2 + 3 x $5 + 4 x $10 = $57
, right? But if you buy thingies first, the cost should be the same, right?
4 x $10 + 1 x $2 + 3 x $5 = $57
This isn’t true if you evaluate it the way you want to, which is why we don’t.
We do the multiplications first, compute the extended cost for each item, then add them together.
Peter: I have enjoyed the videos you produced and have recommended them to some other people. I showed a teacher friend of mine your “tens frame” method and she was instantly convinced of its usefulness.
I think you are exactly right to stress BOTH the importance of knowing number facts by heart, but arriving at this desirable condition via various strategies rather than brute-force memorization alone.
I wonder if you have thought of producing your EBooks and worksheets keyed to the UK National Curriculum (I live in the UK), which I suspect is not very different from the Australian one. Even more ambitious would be to see if they could be adapted to the (variegated) American market.
I have a hypothesis, based on tutoring maths over the last fifteen years to a few hundred children, mainly in the 13-16 range, that even able students, as they are taught maths here, don’t really have a deep grasp of the basics.
If they have been well taught, they have a collection of methods, and can recognize when to apply the appropriate method *if* they have seen examples of the particular problem before. What they seem to lack is any feel for the underlying laws of arithmetic, and the ability to generalize. So they have difficulty in extending their knowledge.
They will know that you CAN “cancel” in this case: (3 x 4)/ 2, and that you CANNOT in this case: (3 + 4)/2, but not WHY. Nor can they see that the latter expression could be expressed as 3/2 + 2.
I’ve been experimenting with trying to teach my tutees some of the more fundamental ideas of arithmetic and algebra, but I’m just stumbling forward in the dark. I wonder if others have anything to say about this?
Thanks again, Doug
We have designed our eBooks to match the curriculum in Australia, the UK and US (Common Core), as closely as we can with one set of resources. In fact, there are broad similarities between all three, so that mostly a teacher can just pick a set that matches the grade or year level they teach, and it should match the appropriate curriculum.
I couldn’t agree more about students needing to have a good, solid grasp of the basics. Like you, I expect, I teach a lot of more interesting and challenging mathematics a lot of the time. But I keep coming back to number facts, place value and foundations of fractions as the first aspects of maths to be mastered by students. Without these basics, I think teaching later maths is pretty well pointless, and moreover likely to result in more boredom and frustration.
I get this wrong every time, I’m 38 and was educated in the UK, I did maths up to A-level (so I studied it in college) and I never once heard the phrase PEDMAS or “Order of Operations”
Basically we were just taught to solve it from left to right unless there were brackets, so in this example, based on my education the answer is 1
Thanks for the comment, Andy.
Wow. I must say I am surprised that you were not taught about order of operations, since it is essential to answer multi-operation questions like the one referred to on this page. Perhaps your teachers assumed you’d already learned it?
Anyway, thanks again for commenting.
Same here ! 2 college degrees, working as engineer for 20 years, I never heard if it either . Solved it same way you did and got the same answer !
I was taught in NC and we were never taught the order of operations either.
I’m finding out among us older people that some were taught it and others were not. This isn’t because we forgot (as some have suggested). We simply were never introduced to the order of operations.
Hi Peter, I am 56 years old and had never heard of bodmas or “order of operations” until I saw your post on facebook, neither had my wife. We both had what we thought was a full education from primary to secondary schools. I attended a grammer school and went on to do three years at technical college.I now run my own small business.
I asked my three sons aged 26. 28. 31. about this and they had not heard of it either.
I decided to look in to this further with an open mind. I studied not only bodmas but the way it has been taught in school, I came across so many conflicting points of view(and so many very angry people). The concencus of opinion seems to be that bad teaching methods or basic misunderstanding has lead to a lot of confusion (it has certainly confused me). I have read reports from some very educated people ranging secondary school teachers to professors of mathamatics with conficting points of view. My wife says I am like a dog with a bone, I won’t let go. So I decided to conduct my own survey, I wrote 2+3×4= on a piece of paper and took around the business park( I got a lot of strange looks). The first 37 people gave the same answer as myself. “20” ( age ranging from mid twenties to early sixties). Not one had heard of bodmas.
The 38th person aged 32 gave the answer “14”. I asked him to explain, He said 3×4 =12 + 2 = 14. I said surely you mean 2+3=5×4=20. His reply “bodmas”. I placed a £2 coin and three £1 coins on the desk and asked how much? he said £5. I did this again three more times, “how much”?. His reply £20. I said “so 2+3×4=20 not 14. He said “bodmas” is not meant for real life, it was just something we learnt at school.
About 2 months later the son(a17 year college student)of one of my employee’s walked into the workshop to see his dad. I asked him the same question, He said there are two answers depending on your point of view. You have expressed suprise, worry and doubt in your replys to some of the comments about whether or not we were taught “bodmas”. My worry is that some people were taught. We have a situation now where two people working on a common project at different ends of the office will make mistakes depending on THEIR point of view.
In your own survey 368 people gave the same answer by working left to right while the rest gave various different answers by using bodmas. My maths teacher told me that the beauty of maths was it’s purety and consistancy, “No matter what language you speak we can always communicate through numbers because there is always only one right answer.
Hi Ron
You get the prize for the longest comment, and the most diligent research into this question. I am truly impressed.
Thank you for your thoughtful, very detailed comments about this question. Once again, I admit to being surprised at what you experienced, and what you found when asking other adults about this topic. As a classroom educator, teaching students in maths class about the order of operations conventions I guess I did not consider how common that knowledge was, it was just a topic in the curriculum. Having taught in primary schools and universities for around 30 years, it has just become something I expect students to know. So to hear that so many adult haven’t even heard of the topic is a surprise.
I have taught in Australia for almost my entire career, so perhaps my experience is atypical on a worldwide level. Perhaps the UK National Curriculum omits the rules for order of operations, which would presumably give rise to your findings among UK adults; I don’t know. I am aware that lots of people commenting on my post here and on Facebook from the US learned about “PEMDAS”, which is another way of referring to the idea, a parallel mnenomic to BOMDAS. So I assume that for many US adults, this is something they learned at some time in their school lives.
The fact is, if a mathematical expression is taken “at face value”, without an everyday context like your coins example, there need to be rules for the order in which operations are carried out, or the result could be ambiguous. As your teacher said, there should be one right answer. And these rules, used by mathematicians and by computer software, are completely unambiguous. Try typing “2+3*4” into an Excel formula and see what you get – it will be 14, because the software has been correctly programmed to handle such potentially ambiguous expressions.
In an everyday context, we need to express the maths in a way that serves our purpose. So in the example of the coins, we understand immediately without hesitation that the correct total value is £20, not £14. But if we wanted to record this as a mathematical expression unambiguously, according to the rules of arithmetic we would have to write “(2 + 3) x 4 =” in order to get the answer which in the real-life context is clearly the correct one. In real life we rarely if ever need to actually record this, so it doesn’t become an issue. But if you study mathematics at a higher level, where it may be a lot more abstract, or where we want to have total clarity in expressing what we mean, we need to follow the rules.
finally the ans is 8 or any thing else plz tell me and i dont know abot bodmas and pamdas and tell me plz …. for this example…7 – 0 + 1 what should be come first addition or substraction to operation on it….
I was considered to be a good math student in high school and after college and graduate school I had a career as a chemist. However when I first saw calculations like the above I got it wrong. Since then I was instructed in this order of operations rule so that now I answer correctly. While I seem to remember other aspects of algebra and analytical geometry well , I have no recollection of learning this rule in high school. I have noticed that when I post such problems, FB friends my age and older get them wrong. While memory issues may play a role, I wonder that this rule wasn’t taught until recently.
Thanks for the comment, Michael. I too am interested about the different response this question has generated among different demographic groups. Maybe this topic is a relatively recent addition to school math curricula; I don’t know. The rule could always be handled using brackets/parentheses, but without them math really requires some rule for eliminating ambiguity.
Thank you for the comment. I went to high school here in the USA graduating in 1965. I did well in math and in my senior year I took an advanced math course that included Boolean algebra and set theory and limits with a very short introduction to calculus. However I have no recollection at all of encountering these rules concerning order of operations. Maybe they weren’t emphasized in the 1960s?
In high school, my teacher did not teach algebra. She regaled stories of when she was sick and how her husband took care of her. I did my nails. I did learn algebra in my 50’s. It took a lot of tears but the instructor and my boyfriend made sure I understood. So I’d say the problem is how they are teaching in school. Fully understanding the order of operations using PEMDAS has helped me immensely. And even a refresher when both of us failed another FB test.
call me stupid, but in all you said I STILL do not get what your answer is and how you got it either…..so yes…….. you guys teach from YOUR understanding…..using terms you know and understand……speak in laymen terms with students talk to them in manner that THEY understand………..your students do NOT have college degrees yet…… could you stop talking to them in college terms??????
. I see the work you did to get to the answer but I do not understand what you did at all……….in order to explain it or do it myself……
Thanks for the comment, BishopDD!
Sorry that my explanation wasn’t clear enough for you. Realise that most who read my material are teachers, so do have a college degree. I really do want everyone to understand, but my general audience is pretty well educated.
With that said, rules for the order of operations are widely taught in elementary school. Here it is, in as simple a format as I can come up with:
If there are parentheses / brackets, start with whatever is inside the parentheses. 8 – (3 + 4) = 1, because you add the 3 and 4 first, then take 7 from 8.
If there is multiplication and/or division, do that next, working left to right.
If there is addition and/or subtraction, do that last, working from left to right.
Examples:
12 – 6 + 4 = 10
12 – (6 + 4) = 2
24 ÷ 4 x 2 = 12
24 ÷ (4 x 2) = 3
2 + 3 x 4 = 14
(2 + 3) x 4 = 20
6 + 3 x 2 ÷ 2 – 4 + 5 x 2 = 15
Actually Bedmas/Pedmas wasn’t taught to me in grade school. (I’m 43) It was taught left to right unless there was brackets in the problem. Then you do the brackets first.
Bedmas was only applicable for higher math problems like calculus or algebra. Not simple Addition/Sub/Division/Multiplication problems.
It’s only been the last 30 years or so that the lower grades (Below High School) are being taught Bedmas. I have noticed many people don’t apply Bedmas because it doesn’t apply.
Also the rule of doing the multiple first only applies if there is brackets. If there are no brackets shown, then it is always from left to right.
If there are no brackets in the problem then you can’t just put them in to make the math go your way. That is the reason we put in brackets to begin with. To tell the person to do that portion first. No brackets means left to right.
Even your calculator will do this from left to right if there are no brackets.
Thanks again for commenting.
Some calculators will operate “correctly” according to conventions, and some will not. Enter an expression such as “5 + 2 x 6 =” and some will get 42, and others the correct answer of 17.
Try it in Excel and it will parse the expression correctly. To me, this is one reason we need to teach the rules in school.
Hello,
I got the answer incorrect. I got 6 so I thought I’d explain where I made the mistake which is different from what you thought. I used the BEDMAS rule: Bracket, Exponent, Division, Multiplication, Addition & Subtraction. The reason I got the answered 6 was because I stuck strictly to the BEDMAS format which had me do the addition before the subtraction. I had forgotten that you do addition & subtraction at the same time (left to right). My only excuse is I’ve been out of school for some time now.
Hi Tim,
Thanks for the comment. To me, that is a really smart mistake to make, because the BEDMAS rule appears to say “Do division then multiplication then addition then subtraction”. But division and multiplication should be grouped together, and so should addition and subtraction.
Maybe something like BE[DM][AS] would help, but it’s harder to read.
I am glad to say I learnt the order of operation like this PE [DM] [AS] my math teacher drew little arrows below the D and M pointing → and little arrow below the A and S pointing →. He emphasised that if there was more of any one in the brackets you calculate left to right. This image stuck in my head and now whenever I see an equation first thing I think is that image. Needless to say I have done well with mathematics in my life and have got this equation correct. It’s hard to explain to others how this works but it all makes perfect sense to me. My teacher was Mr Carter. He also had funny jokes he made horizontal easy for me to remember – I’m from New Zealand. Please take this with a grain of salt. What do you call a lying down Maori? Hory-zontal. Made me and my class of Maori students laugh. He was great. I was also one of those tough students who never paid attention in class but his techniques helped me remember even though I wasn’t intentionally paying attentions.
Thanks for the comment, Adrienne – it made me laugh!
I am thrilled to hear of students who learned math from a teacher who helped them to remember it. Jokes to help you pay attention are a bonus.
The idea of putting M & D in brackets with an arrow below, and the same for A & S, is excellent. I’m glad it worked for you
I’m no teacher by any stretch of the imagination, but was still outraged by the responses I saw on facebook. I believe the “6” answer comes from either reasoning stating in previous posts or from people simply thinking 0s can be thrown out as (1×0) may be read as +(1×0) = 0 and since 0 is neither positive or negative, it gets thrown out, leaving 7 + -(3÷3). In algebra, I tended to read numbers in equations like this as we would generally be moving them across the equal sign in the coming steps. Attaching the sign with the immediately following number made things much easier for me. Since this was done years after learning PEMDAS, it may have replaced that way of thinking in many people. I know when to use each, but many people just “replace” ideas learned in elementary school with new methods learned to tackle advanced mathematics in high school. If had a dollar for every time a teacher told me “forget everything you learned in middle school, I’d be able to order a couple of pizzas.
I think my last comment got stuck in cyberspace somewhere.
I am no teacher in any stretch of the imagination, but my theory on 6 answers seems logical (mostly because it’s how I think). I was taught PEMDAS in elementary school and grasped the concept quite well as most students in my class did (including left to right). As I read this equation on Facebook, I default to algebra and then realized there were no parenthesis, so PEMDAS took over and I was able to decipher 8 from the garble.
As I posted my answer, I was flabbergasted by the amount of “1s” I saw! As I went back over the equation to find out how 1 could be obtained (and to second guess myself), I realized they simply didn’t apply any sort of Order of Operations. I then saw a fair amount of “6s” as answers and people reassuring everyone else they were using PEMDAS or BODMAS, so I went back to the equation out of curiosity (and to third guess myself). After staring at the screen for some time I realized that people were just tossing out the 0 altogether. In Algebra, I found myself attaching the addition and subtraction signs to the immediately following numbers in preparation of moving them around and across the equal sign. If this logic was applied to this equation, one might arrive to 7-(1×0)+(3/3) and in their minds, see -(1×0) and +(3/3). When (1×0) becomes 0, they throw the 0 out because “it’s zero and not important.” Then all of a sudden you have 7- +(3/3) equaling 6 when it should be 7+ -0 + +(3/3) if you’re using that logic.
I believe this stems from the linear track we take in school. I learned PEMDAS in elementary school and when I got to middle school and started algebra my teacher told us to forget everything we learned in elementary school, because it would confuse us. The teachers throughout high school did the same thing and “replaced” foundations with these new ways when they should have been nurturing the foundation and adding to it. I was lucky enough to keep the foundation stored away somewhere, but many people get overwhelmed and just want to pass the exam, so they learn what they need and forget what they don’t.
Hey Josh, thanks for the comment.
Your first post wasn’t lost, it got stuck in a moderation queue. Like most blogs, we get spam comments, so I moderate all comments.
As a previous elementary teacher, I am disappointed in the message that middle school or high school students should “forget everything they think they know”. Well done for figuring out what was important on the way through!
Hate to sound like an uneducated so n so (mainly because actually I’m not, but I’m no mathematician either) but surely as we read and write from left to right the most logical order to do any equation is left to right regardless. Unless of course there are brackets involved in which case common sense tells you to work those first. I was taught BODMAS and got the answer wrong due to being out of school for 12yrs and not using mathematics like this in adult life along with 74% of others who also got it wrong, thus proving maybe that order of operation is pointless as the MAJORITY of people will never use it again after leaving education. I mean, lets face it, how did this order come about anyway?? Some bloke sat down one day, wrote some sums and thought “ok, you can do it this way and get this answer…or…you can do it this way and get this answer…yeah, lets go with the most confusing, it’ll make it look more impressive! And anyone who gets the other answer is wrong…spread the word”. Collectively agreed or not, it doesn’t seem like the most logical format! Just a thought.
Thanks for the comment, Kirsty. I don’t have any answers for you, other than what I’ve expressed on this page previously.
Clearly, the rules for handling multiple operations in a single expression are not well known. And yet they are not that complicated.
The other point I think you are alluding to is that for most of us, these rules just aren’t that important, and we manage to go through life quite effectively without them. I agree. But in some situations someone has to know how to do it or we’ll get the wrong answer. So we keep teaching the rules at school.
I feel that there are several issues in teaching order of operations in school. The first issue is an issue of education in general. We coddle our children. We allow them to too easily forget what they have learned and allow ourselves to continuously reteach these concepts each year. Students recognize when we as teachers start the year with a big three week review that they don’t have to try and remember from year to year what they’ve learned. We’ve not set the retention bar high enough.
The next issue is these students who don’t know to do the parts of it correctly. I think that in many cases, the way we stress the acronyms is causing an issue. PEMDAS implies you do addition before subtraction. PE(MD)(AS) groups the order in such a way that you know there is something special when you get to multiplication/division or addition/subtraction.
Thanks for the comment, Kaitlyn – I agree with you.
I think the main problem with this is not the content we are trying to teach, but the “dumbed down” acronym most teachers use to teach it.
I read a while ago that it’s common practice in New Zealand to teach the PEMA acronym, which I think helps to avoid confusion over operator precedence, particularly when students are shown examples of multiplication and division of integers by decimals.
John, thanks for sharing. That sounds like a good idea. It removes part of the problem, which is students assuming priority of addition over subtraction, and multiplication over division.
I was never taught Bedmas in grade school. I was taught that in simple math equations the order goes from left to right unless there is brackets in it. If there is you do the brackets first and then the rest from left to right. If there is no brackets then you go left to right.
From some of the posts in forums from mathematicians, they have stated about the common misconception (Mistake) of Bedmas being taught for simple math.
They state it should only be used in higher math forms like Algebra or Calculations when the equations get more complicated, and no simple math equations like the one in the above post.
Sorry but the reason over 70% of the people get it wrong is because Bedmas doesn’t apply in simple math. Not because it does at all times.
Thanks for your comments.
This has always been a tricky topic for elementary / primary teachers, because it is difficult to learn and it actually has few applications. Most of the time we either use brackets / parentheses or the order in which operations should be carried out is obvious or unambiguous.
With all that said, an expression such as “4 + 2 x 6 = [___]” must either follow some convention (rule) or is ambiguous. You simply cannot say “the rules for order of operations doesn’t apply to simple math/s”. Since we don’t want ambiguity, even with a simple expression like this, and since if you enter the expression into some piece of technology you need to know if it is being calculated according to our conventions, we must have a rule or we cannot answer the question.
The idea of working left to right apart from cases with brackets or parentheses is attractive but wrong. We DO give priority to multiplication and division over addition and subtraction, whether or not we prefer to just work left to right. So, again, we need the rules for those cases where we have two choices.
I SO agree with you, GGHammer and Nancy Spencer! I’m 67 ….. and I never HEARD of “order of operation” all through high school …. and I don’t recall being required to take any advanced math classes in college. ( So I didn’t!!) I was an Early Childhood Educ. major …. so there were classes on how to teach basic arithmetic to elementary school kids. Left to right unless there are parentheses. Period. I never actually taught, so I assume I might have been exposed to different ways of teaching math as the years went by. I pursued a different career path involving language arts. And I never met Aunt Sally or her cousins BEDMAS et al, athough now I CAN see how the “correct” answers are found. Calculators weren’t used in any class I ever took through college (bought my first one at about age 25) ……and computers were only used by ….. I don’t know …. NASA?? And they took up entire rooms. 🙂
I don’t know the averge age of Facebook users, but I suspect the percentage of “wrong” answers (74% per Peter’s “disappointing” graph results) has at least SOMEthing to do with age. I have friends in their 80s who use Facebook …. as well as twenty-somethings. All I know for sure is that I resent any implication …. by ANYone …. Peter! …… that I am ignorant or uneducated because of the way I was taught to approach math prohlems! Granted, I only have a B.S. degree but graduated Magna Cum Laude.) On the other hand, this discussion, here and on FB, is fascinating. And I, too, would love to know when PEMDAS was introduced into elementary school curriculums and whether it hit all U.S. states simultaneously or started out only in California or something. Getting off my soapbox now. 🙂
I’m 60 and learned this probably in 62 or 63 in elementary school. I remember being taught that you worked from left to right and if there were no parentheses, no PEDMAS (or whatever.) Did use it if there were parentheses. ;My brother learned it the same way. He has his PhD, is a college professor and also associate dean and acting chair, he is very smart. I just asked him and he still says if no parentheses, work left to right. He got through all of his college, masters, PhD, etc. and even graduated with honors. I went to some college but got through with a’s and b’s, and never encountered this. My actual question is, how were so many of us taught “wrong” in elementary school, or (as I have heard from some people), we were actually taught this way, but the curriculum changed after or in the 60’s when computers came in to play. Is there any way to find out when this happened, or did we just happen to have an awfully lot of teachers just teaching it wrong? (Well, it’s wrong anyway, but I guess rules not enforced?) Is there any way I can find this out? Thanks!!!
Hi Nancy
Thanks for the comments! I am surprised at stories like yours and your brothers, of never being taught these rules, ever. I just thought everyone would learn them at some point in school.
It is fair to say that the need for the rules arises rarely, so most people could go right through schooling perhaps to doctoral level without noticing or really needing to know and apply the rules correctly. If I had been your elementary teacher, I would have taught you the rules at some point. And had you asked “Sir, why do we need to know this?”, I would have shown you a question such as “7 + 3 x 4 = ” and asked you what the answer was. Since we cannot tell whether the answer should be 40 or 19, we need rules of precedence. The alternative is to insist that ambiguous expressions have brackets / parentheses inserted, but we don’t do that.
To me the biggest problem here is not the rules themselves (we don’t get to pick what we are taught at school, or what we should teach), it’s poor learning of the principles. Rather than teaching some attractive but possibly misleading acronym such as “BOMDAS”, “PEDMAS” or “BIMDAS”, we should teach students that multiplication and division are more important that addition and subtraction, so we carry them out first.
To return to your question, I learned the rules at some point through my schooling, like you in the 60s and 70s, in the UK and Australia. I do not accept that these rules are a recent addition to mathematics, added erroneously by elementary teachers or curriculum writers. We simply wouldn’t have come up with these rules if mathematicians did not use them and they were incorrect. Curriculum documents change significantly over time, so it is plausible that decades ago the rules were never taught because they were not felt to be important enough. But the idea that they did not exist does not seem believable to me.
I’m a 31 year old guy from the UK. While I don’t specifically remember “BEDMAS” or the US equivalent being peddled in school, I definitely remember being taught some order of operations. I too achieved the correct answer. I’m fascinated by the ambiguity on this kind of scale. It astounds me. I guess I am in a slightly different position to most – while being ratified as a superior intellect, I labour in the building industry, so don’t often get to see this kind of thing and can vouch for the large percentile of people that will never need to.
For general day to day living, I’d say that simply being aware of the context of the math you are solving is enough. As in the example above with the 2+3*5 is not the same as £2+£3 * 5. Even when doing some rather technical excel work, I rarely have a use for (mentally), needing to know that powers comes first. It’s very rare that parentheses, exponents and even multiplication/division are required in a situation where you wouldn’t have a calculator or a computer to hand. The last time I had to deal with exponents was around 2 years ago, when working out some betting calculations, and even then, had my smartphone to hand to do the math for me.
I do believe however, that a universal system should be adopted and taught. Even as something as simple as knowing that multiplication and division are “harder” than addition and subtraction, and exponents harder still could be distilled into teaching students to “do the hardest bits first” or something more eloquent. If at least the context of maths is lost, and the instantly forgettable BODMAS/PEMDAS systems and forgotten – it could stick in the back of the mind.
Hi John, thanks for your comment.
I have just left another comment referring to your money example, since Nicholas mentioned it also. I don’t think your example demonstrates that the rules are flawed.
I find using Excel either I need to recall the rules for order of operations, or I have to use brackets / parentheses in order to get the result I want. So to me, the rules are directly applicable to this task, and not knowing them will make entering formulas more difficult.
I think using the BODMAS system is stupid.
The answer is 1.
Or do you think i should send my qualification back from 35 years ago.
I was always taught to start from 1st number in the sequence and do each calculation separately unless there were numbers in brackets which were done first then start from the 1st number in the sequence.
Hi John, thanks for the comment.
Stupid or not, we have a situation where different methods lead to different results. Since in mathematics we don’t accept the idea that there can be multiple correct results for a simple equation, we need rules.
But of course, however much we may like the way we do it, or the way our favourite teacher taught us, etc., for us to have accurate communication of mathematical equations, there has to be a set of rules that is universally agreed (by those qualified to make that decision) to be correct.
I don’t like BOMDAS or BOMDAS either (as I’ve explained above), but the answer is not 1.
Whether or not you should return your 35-year-old qualification is your call. 🙂
All flippancy aside, however, I mean no offence to anyone. I am simply trying to point up the confusion that exists in the minds of many of various ages about questions like this.
This is an issues I have come across recently. I am 29 and British and have not heard of bimdas until this Facebook post came about. I was taught that brackets give present then work left to right to work out the sum. The comment using money proves that bimdas is fundamental flawed in the real world so why is it used today? And if it is so important why does it give an answer that is wrong once applied outside of a class room.
Hi Nicholas! Thanks for your comment.
Is BIMDAS really flawed? I guess it depends on whether you agree that it produces the correct answer or not.
My answer: it is not flawed if you use it absolutely correctly. But many are confused about how to actually apply it, and so it doesn’t actually help much. As an educator, I use other approaches that take longer to explain than a simple acronym, but are more accurate (IMHO).
The comment above from John was ” 2+3*5 is not the same as £2+£3 * 5″.
Well, as others have stated, the correct answer to the question in context will depend on the context. If I say “I’ll give you £2 every day if you clean your room and £3 every day if you take out the garbage”, then the expression *could* describe the maximum amount of money you’ll receive over 5 days. But not really, since the rules of arithmetic attach higher priority to multiplication, so we need to add brackets / parentheses, and write “(£2+£3) * 5”, for this to give the correct answer of £25.
So, I would argue that “2+3*5 IS the same as £2+£3 * 5”. And the answer would be £17
You say I . But not really, since the rules of arithmetic attach higher priority to multiplication, so we need to add brackets / parentheses, and write “(£2+£3) * 5”, for this to give the correct answer of £25.
Surely it would be written as (£2 *5) + (£3*5) then using either BOMDAS or not it gives £25
Also I was taught that when you have different units in an equation you deal with them separately so you deal with the £`s and get £2+£3 = £5 then multiply by 5 giving 25
I graduated high school in 88’ and I took basic math and never took algebra because it wasn’t a required course. I was never taught this form of math. I, like other commenters was taught to do the problem left to right unless there are parentheses. I had to look up what everyone was talking about because I had never heard of it and couldn’t figure how others were getting a completely different answer from what I was getting. I makes no sense to me why the education system is making math so complicated. It’s is assumed that you will assume the correct order in which to do the problem however if you haven’t been taught the “assumed” way of math you will get the answer wrong. The reason so many on Facebook got the answer wrong is because they, like me, are older and if they didn’t take algebra in school wouldn’t know the “assumed” order of how to do the problem because they were never taught the process.
This is just a personal thought. And I stand to be corrected here Dr. Price.
After so many arguments on a repost of that equation on Facebook I Google searched 7-1×0+3/3 and found the bugger that instigated all this was you (pretty fun though).
Dr. Price, your equation raises alot of question on when and where the Order of Operation should be applied, and whether or not people still do remember BODMAS/PEMDAS.
Personally for me, this equation and you explanation on this page has prompt me to ask this question:
*Should All Mathematical Rules, Principles, Procedures, etc. be revisited or questioned or tested before it could be taught in schools?
I only ask this question because what if at any point in time an equation arises and cannot be solved whilst working within the perimeters of the already established mathematical rules and principles.
-How can it be solved?
-What principles should we apply?
-What if it threatens the very core of the established mathematical rules and rendering it to become redundant?
Furthermore, I applied this equation to a scientific calculator and the answer was 8. Which means the mathematical principle of solving arithmetic equations was centred around the Order of Operations.
Therefore, it the event that such a problem resulted, and new mathematical principles or rules are applied, that would render certain principles/rules redundant. Also, mathematical devices such as calculators and applications would become redundant henceforth.
Anyways, my answer for your equation is 8.
Being 43 and educated in the UK, I was never taught BODMAS (or BIMDAS, BEDMAS, BIDMAS and PEMDAS) at any point in all the years of school. Therefore until these things started popping up on Facebook and other places I have all ways done any maths (yes thats what we say in the UK not math) as written. I feel a bit let down with my education and a possible reason I ditched A level Mathematics as I had no clue!
Hi Peter, great article! Really stimulating.
I am 32. I am an electronics engineer. Until I saw a Facebook post with one of these questions, I had never heard of BODMAS or “order of operations”. As part of my job, I solve long, complicated equations of this nature on a regular basis and have NEVER (don’t mean to shout, phone won’t do itslic) had a major problem.
I responded to the Facebook post and received a reply from a somewhat irritated individual. A discussion insued and since there were enough mentions of BODMAS to cause me concern, I began to investigate with an open mind. I did Internet research (how I got here) and also asked colleagues and friends. Thankfully, most of my colleagues did know BODMAS. Almost no-one else did. Interestingly, my 16 year old nephew did know BODMAS, yet he still got the same answer that I did.
As an engineer, I’m often accused of being pedantic. I believe that in engineering and mathematics, accuracy and semantics are crucial. As such, I fully agree that we need rules to eliminate ambiguity. However, u strongly feel that “left to right, solving brackets first” is a far simpler rule than BODMAS fir several reasons :
1) As mentioned earlier in this thread, we read from left to right, so it seems logical (I think most would agree)
2) Even with the BODMAS rule, we still need brackets, so why have more rules than necessary?
3) As mentioned earlier in this thread, BODMAS “implies” that division comes before multiplication, and addition before subtraction. Whilst I accept that this is likely due to poor teaching methods, it can’t be denied that it is a complication that often causes error.
4) MOST people work left to right, solving brackets first. This seems to have been taught more than BODMAS. Why is this wrong and BODMAS right?
This is one of those subjects where people are often firmly planted one side of the fence or the other. This is just human nature – we are comfortable where we are and instinctively reject change. I admire all the commenters on this thread for being civilised and non – confrontational (unlike most of the Facebook comments I’ve seen). I make no illusions that I am not on the fence on this subject. I respectfully suggest that you are also pretty confident which side you are on. As I said previously, I’m keeping an open mind. Currently, I see no value in BODMAS over “left to right, brackets first”. Nevertheless, I welcome a constructive, logical justification.
Keep up the good work and thanks for giving my brain a workout. 🙂
Pete, thanks for your carefully considered comments. I appreciate that you believe in accuracy; as an engineer that’s obviously an important part of your work.
I’d love it if we could just say “work left to right, do the brackets first”. However, others before you and me have said that multiplication and division take precedence over addition and subtraction, so a question such as “4 + 5 x 8” cannot be done left to right and get the correct answer. We could insert brackets everywhere there could be ambiguity, but with the rules of precedence (order of operations, as we often call it), we don’t need the brackets.
Thanks again for your input into this discussion.
~ Peter
How is 4 +(5×8) any more ambiguous than 4+5×8
Raymond good point. I meant “if there were no rules for precedence of operations”, then we could evaluate the expression in two ways producing two different results. Thus, ambiguous.
What amazes me is how many people who got it wrong were not only sure they got it wrong, but were telling others how stupid they were for having a different answer. While I’m not shocked a lot got it wrong I am shocked how few actually had correct. For these types of questions it wasn’t particularly difficult. Throw in a couple of exponents and it would be fun.
Quite worrying actually Peter. This is why I teach basic maths to my girls. As a result, both my girls are A students in maths. What concerns me, is when people say, “That’s how I was taught at school”. Either they were incorrectly taught or were taught but don’t remember, as not everyone are mathematically inclined.
Thanks for your input, Andrew. Well done on helping your daughters to excel at maths 🙂
One of the Best things I enjoyed learning about mathematics in the 1960 were logarithm tables. BODMAS/PEMDAS. were not taught to me and mathematics was step by step, left to right in order. Log Tables were a Joy in Multiplication & division were replaced by Addition & Subtraction. If Brackets are Used Yes They are process first. If not Simple math is what I was taught to apply applies. At the end of High School, Calculators were available in the Classrooms. Interesting enough a Question in my Final Exam a question was marked incorrect because of the Calculator rounding down pi in a Geometry question. Happy with 199/200 Questions Correct.
I am 79 and thought I was reasonable at arithmetic, had to go to Google to find out what the heck BODMAS, never heard of it at school, and had a gorgon of a maths teacher in secondary school, if you asked for something to be repeated her normal response was lochgelly tawse, and ” you don’t listen!” that was my first class of algebra, I think now in hindsight, she was not good at teaching her subject, definitely put me off maths for life
Born in USA but raised in other countries (military brat), as kid I was taught to do math ‘Left to Right’ then I finally came back to USA Nevada during my junior high and high school years. I struggled hard in math because of the answers I was providing not correct. NOT a single one of my math teachers would explain this to me or even walk me through the problems but just fail me or push me back a level class. Now years later using a mobile phone calculator to calculate 70-26÷7 (for financial reasons) and the answer I got was 66.2857142857. I thought it was incorrect and did it on my computer and got a different answer 6.285714285714286 , so I google it and got to this page where everyone is explaining BODMAS/PEMDAS… I never even heard of this tho it now explains why I been failing. I’m pist beyond belief on held back I was because this critical lesson wasn’t even taught to me, I even called up my best friend from high school and asked him and he was confused on what BODMAS/PEMDAS was. Years of time wasted and opportunities missed.
Wow, David, that’s quite a story. I am sorry to hear that apparently you had a gap in your maths education. It seems amazing to me that such a thing can happen, given that a simple question like “12 – 2 x 3 = ?” clearly has two possible answers, unless there is rule to follow.
Thanks for the contribution to this discussion!
You are an idiot. NO ONE uses BODMAS anymore, stop quoting that out of date shite and confusing students. If you are a maths teacher you should be shot.
Wow, John, tell me what you really think.
I’m guessing I hit a nerve somehow. And I’m guessing you are not a teacher. Fine. But you are wrong about the number of teachers teaching BODMAS. It is in the curriculum: EVERY teacher of the relevant grade levels teaches the rules for order of operations. And many, many, many teachers will use mnemonics such as BODMAS to help students to remember the order.
Now, if you are a mathematician, or other university/college professor, I understand it if you feel that teachers like me are dumbing down the math when we use memory joggers like BODMAS, and I will respect your viewpoint if you express it with a little humility and courtesy.
Hi Peter
Also didn’t learn order of magnitude
Parentheses first then left to right.
I think if equation had parentheses it would not have thrown so many off
I too came up with 1 for answer. Until I relooked at it. Then answered 8.
Never heard of any of the acronyms thanks for the fun
Joann
I went to high school in the 40’s. And not taught order of operations so I found all of this fascinating. I was just simply taught “ if in parenthesis do first”. What I do remember is my children coming home with “ new “” math and when I checked homework I did it my way which was a half page shorter. It was enlightening to read comments and your patient answers. I can honestly say I don’t remember a time in my life I questioned how I used math and In my job I did many budgets working with government grants that depended on accurate statistical analysis. So I must have had good teachers or just learned it a different way. But from all the feedback you’ve received and from other articles Ive read- there is no standard for all schools. This country needs a standardized education system in this country. Not only for math, but for all subjects.
I only discovered BIDMAS when teaching engineering at College. Oddly enough, I’d been doing it “right” all my life (near 70 years). I think BIPS (or BOPS) is the way to go. Brackets, Indices, Products (left to right), Sums (left to right). So for something like 3×4/2 – 2×4/2 +1 = ? do the Products, each l-r. 3×4/2 = 12/2 = 6 and 2×4/2 = 8/2 =4 which now gives us a Sum of the form 6-4+1 which equals 3 however you do it, and l-r is simplest. Just to be clear, I can’t type a 2-dots-and-a-line division sign so have used the slash instead. As far as the terminology is concerned, 3/2 is the same as 3 x 1/2 [a product], and 3-2 is the same as 3+ (-2) [a sum].
I went to a country NSW Australian school in the 50s. as did my husband..We were taught the left to right method up till year 10. My son left school in the 80s and does maths the same as us. Our other 3 children were taught Pedmas as were at school in later years. My husband was a bank manager in the days before computers and was a whiz at maths. Although not Pedmas..
I think its obvious from the comments from many educated and highly regarded professionals , that the BODMAS system was missing from their education . I for one would have read such an equation from left to right , having first addressed the powers and parenthesis had they been there . At 57 years old , I openly admit that today is the first of me ever hearing the term BODMAS . These equations that are put on places like facebook , are designed to do exactly what they have done , create argument , debate and controversy . When all is said and done , I do not believe that any mathematician or professional in this field would ever write an equation like this without brackets or parenthesis , unless they were trying to court an argument . PS Maybe I should also throw out my calculator .
I’m 59 years old and grew up in the UK.
I was top of the class at maths and studied maths at A level.
I have never been taught BODMAS, BIDMAS or PEMDAS.
These methods were only added to the UK general curriculum as required learning in 1988.
This has resurfaced again, as it does so often, when a mainstream newspaper or a person much followed on social media posts one of these “ambiguous” conundrums. In looking at the wrong answers given, I’ve noticed that BO[DM][AS] is being applied alongside other techniques taught in mathematics, such as “implied multiplication” which had been taught as part of common factors and distributive properties. Order of operations is a stepping stone on the path of the mathematical language – it’s beautifully simple and fairly easy to remember, but it doesn’t cover more complex mathematical notation, such as factorials, absolutes and common factors. Are children not being told that this is NOT the be-all and end-all of the maths toolbox?
If this ‘operation’ sequence was introduced in 1923 and considered to be the ‘bees knees’ of working things out, WHY OH WHY has it not been taught in every school throughout the world to the exclusion of sequential working out ever since. It has left generations of people completely confused! It begs the question – “Was it just a wry hoax after all?”.