This week, my wife and I are in South Korea to visit family.
I have noticed when visiting museums that I am often able to use math to make sense of information that is presented in Korean, a language I don’t speak.
For example, we visited Gyeongbokgung, the Korean royal palace from the 14th Century, in Seoul. In the museum next to the palace grounds was a large wall chart in Korean, showing the Royal family tree up to 1910, when Japan annexed Korea and the royal family was dissolved. Look at this section (click for a larger image):
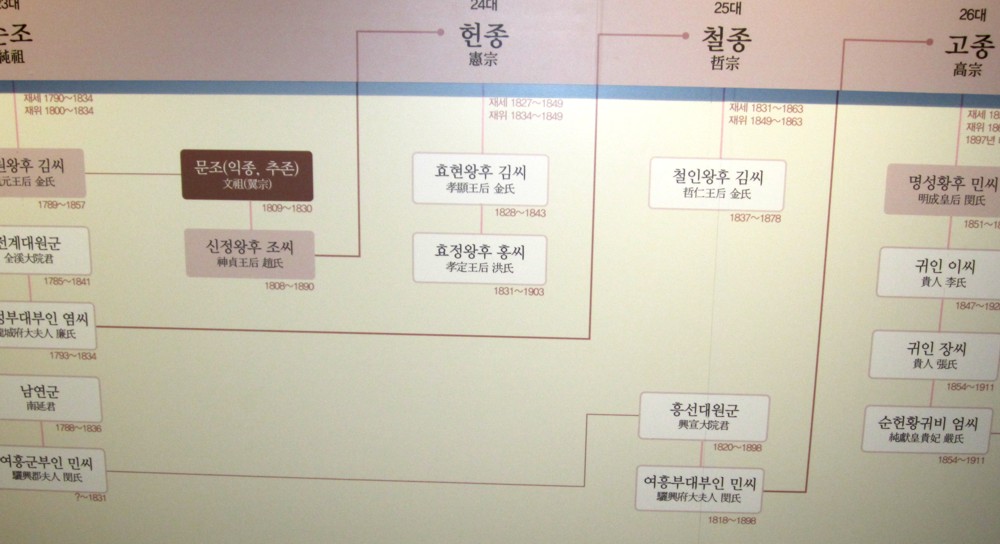
Korean Royal Family Tree 1790-1863
Unless you read Korean script, at first glance this will appear almost unintelligible. But with a little deduction, there is actually a lot of information which may be gleaned from the chart.
Click the photo above for a larger image. Each box has a pair of dates under it, noting the years of birth and death of that person. What can you learn about the Korean royal family in the 19th Century? The detail that is available to us using quite elementary math is surprising.

The study of history gives an excellent opportunity to put to use mathematics skills to learn more about the people being studied. Here are just a few pieces of information deduced merely from the dates provided and the graphical layout of the information:
- Looking down the left-hand vertical column, birth dates are 1790 (the King), 1789, 1785, 1793, 1788. These people were thus of the same generation, since their birth dates were only a few years apart.
- The six people in the left-hand column are in pairs, and each pair is linked by a line to an individual in a column to the right – obviously a couple’s child.
- The person represented by the dark brown box was born when his parents were 19 and 20 years old, married someone approximately a year older, and they had a child when they were 18 and 19 years old.
- The child became the 24th king at age 7, and reigned until the age of 22. In fact, the throne had skipped a generation, and the 24th king took the throne in the place of his grandfather, his father having already passed away 4 years earlier. His mother, on the other hand, outlived the king by 41 years. His grandmother also outlived him, and was 45 years old when he took the throne.
I wrote previously about using math in a visit to a graveyard to learn about the history of the people interred there. It is quite amazing how much one can learn using math in a similar context, even when the rest of the text is in a foreign language!
If you would like to use other photos from this museum to give students an experience of finding information using math, download the accompanying zip file containing 5 photos:
How do you use math in history classes? Feel free to leave a comment below.

Hi,
I am a mathematics teacher for Cambridge IGCSE (9-11th grade) and Advanced (12-13th) Levels. I am very impressedby some of your techniques, which have greatly influenced my teaching style. However, I would like your advice on one topic. Where I teach, all the students take Mathematics as a subject in their O levels and IGCSE, with some of the more proficient ones taking Additional Mathematics. Of these, approximately 70% of the students continue Mathematics in their A levels, and 4% take Further and Higher Mathematics as well. However, the IGCSE course is much simpler in structure, learning and application, and is centered around guided learning. The Advanced level is much more intense, conceptual, and with a complex structure, placing more responsibility on the student. As a result, the transition to the A level is very hard on the students, and even the brightest can buckle under the pressure. How would you recommend I soften this transition?
G’day, Yaqoob!
Thanks for the question. I am not sure how well I can answer this question, but I’ll give it a go.
To my mind, the most important part of doing well in mathematics is understanding it. This starts at the earliest ages, and is relevant for students at every age. By “understand”, I mean that the student can make connections between the current topic and previously-learned mathematics, and can recognise applications for the mathematics in other settings. (At the youngest ages, these settings will be familiar everyday contexts, but for older students they may be applied settings, perhaps connected to other subjects such as technology, computer programming or science.)
The point at which you can best help the students “transition” as you describe, in my view, would be at the point of setting up their “mindset” for doing mathematics. In other words, talk to them about their attitudes to math/s, their reasons for studying it, their ability to think metacognitively about what they are doing. It is critical that they can figure out connections for themselves, and figure out how to solve new problems. This is always true, but especially so at the highest levels of study of maths.
The alternative, which I hate with a passion, is to learn how to apply regular routine procedures to carefully constrained sets of problems, and memorizing which procedures apply to which sets of problems, and how to apply them, all without attempting to understand why it all works. This is a bad idea for younger students or those studying easier maths, but is a disaster to anyone genuinely trying to understand advanced mathematics.
If I were in your position, I would spend a fair while working on students’ thinking and mental attitudes towards doing mathematics, encouraging them to “own” the learning for themselves, and take on responsibility for developing the necessary mathematical thinking.
I hope this helps! Let me know what you think.
Thanks for the reply! I have noticed that the students with an intuitive understanding of the subject rarely encounter problems, and most of their errors are due to simple arithmetic mistakes. Whereas I, too, feel that the best way to teach mathematics is through understanding, some of the graduate from the lower classes with formulae and methods memorised, especially in topics such as basic differentiation and integration. This mau be efective for the junior examinations, but is useless when the students enter advanced classes, where the questions are more conceptual. I will try your approach with my current transitioning class, as they have almost 6 months before their decisions, and see how it goes.